An improved compact embedding theorem for degenerate Sobolev spaces

Abstract

This short note investigates the compact embedding of degenerate matrix weighted Sobolev spaces into weighted Lebesgue spaces. The Sobolev spaces explored are defined as the abstract completion of Lipschitz functions in a bounded domain Ω with respect to the norm: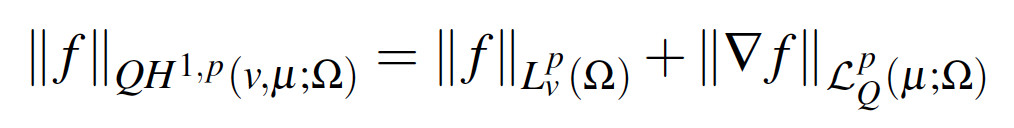

where the weight v is comparable to a power of the pointwise operator norm of the matrix valued function Q=Q(x) in Ω. Following our main theorem, we give an explicit application where degeneracy is controlled through an ellipticity condition of the form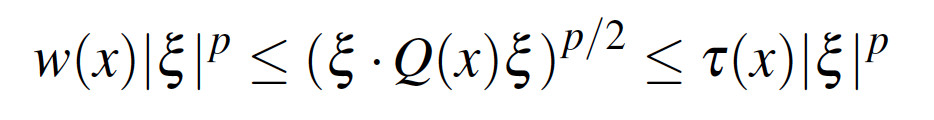

for a pair of p-admissible weights. We also give explicit examples demonstrating the sharpness of our hypotheses.