On the Harmonic characterization of domains via mean value formulas
Abstract
The Euclidean ball have the following harmonic characterization, via Gauss-mean value property: Let D be an open set with finite Lebesgue measure and let x0 be a point of D. If
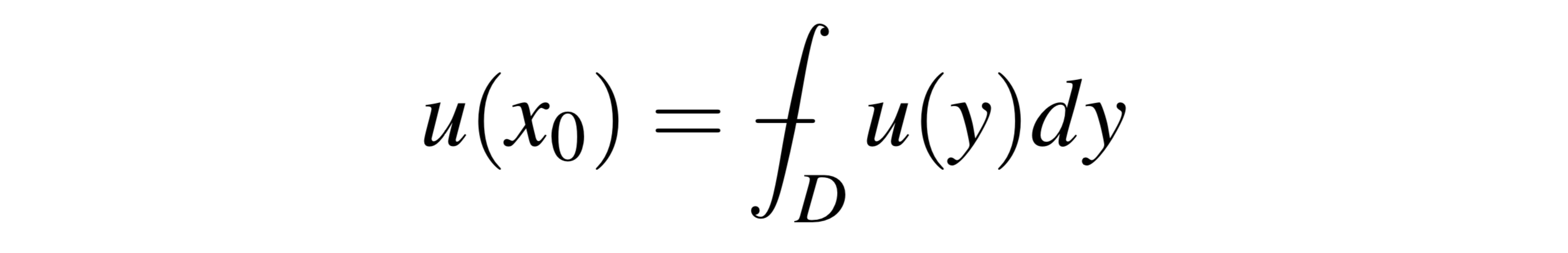
for every nonnegative harmonic function u in D, then D is a Euclidean ball centered at x0. On the other hand, on every sufficiently smooth domain D and for every point x0 in D there exist Radon measures μ such that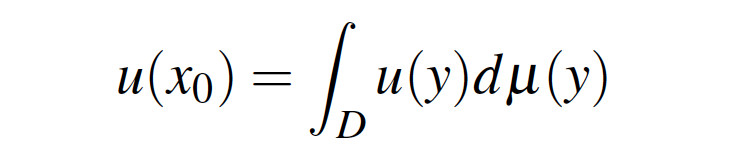
for every nonnegative harmonic function u in D. In this paper we give sufficient conditions so that this last mean value property characterizes the domain D.
Downloads
Published
Issue
Section
License
The authors retain all rights to the original work without any restrictions.
License for Published Contents
"Le Matematiche" published articlesa are distribuited with Creative Commons Attribution 4.0 International. You are free to copy, distribute and transmit the work, and to adapt the work. You must attribute the work in the manner specified by the author or licensor (but not in any way that suggests that they endorse you or your use of the work).
License for Metadata
"Le Matematiche" published articles metadata are dedicated to the public domain by waiving all publisher's rights to the work worldwide under copyright law, including all related and neighboring rights, to the extent allowed by law.
You can copy, modify, distribute and perform the work, even for commercial purposes, all without asking permission.
No Fee Charging
No fee is required to complete the submission/review/publishing process of authors paper.


