Singular quasilinear problems with quadratic growth in the gradient

Abstract

In this paper we consider the problem

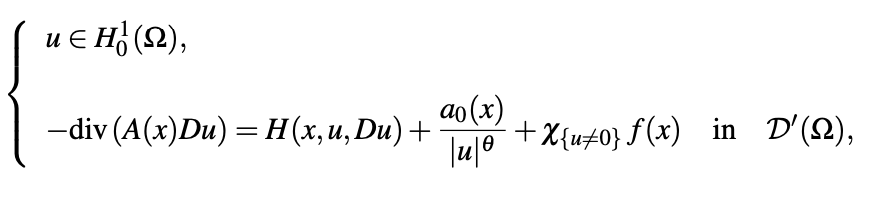
where Ω is an open bounded set of RN (N ≥ 3), A(x) is a coercive matrix with coefficients in L∞(Ω), H(x,s,ξ) is a Carathe ́odory function which satisfies for a given γ > 0 and some c0 ≥ 0

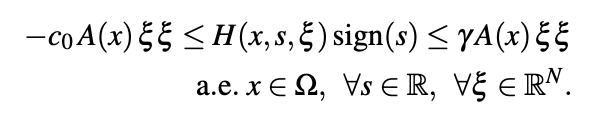
The nonnegative term a0 belongs to LN/2(Ω), χ{u̸=0} is caracteristic function, f belongs to LN/2(Ω) and 0 < θ < 1. For f and a0 sufficiently small (and more precisely when f and a0 satisfy the smallness condition (2.11)), we prove the existence of at least one solution u such that eδ |u| − 1 belongs to H01(Ω) for some δ ≥ γ. Some a priori estimates are obtained.