Asymptotic behavior of solutions for parabolic problems of fractional type and sign-changing measure data
Abstract
We prove a new asymptotic behavior result (with respect to the time variable t) of entropy solutions for fractional parabolic problems, with Dirichlet boundary at infinity, whose model is
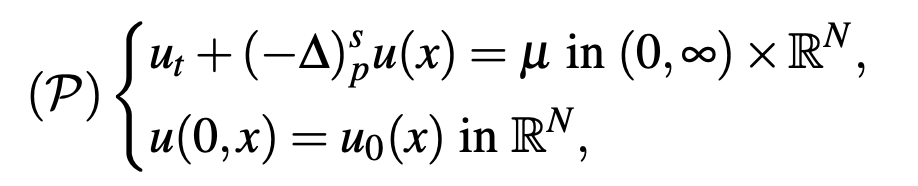
where (−∆)spu is the fractional (s, p)-Laplace operator (with ps < N, 0<s<1 and p>2− s), u0 ∈L1 (RN) and μ is a bounded, compactly supported Radon measure whose support is compactly contained in Q := (0, ∞) × RN , N ≥ 2 (not depending on time) which does not charge the sets of the fractional (s, p)-capacity.
Downloads
Published
Issue
Section
License
The authors retain all rights to the original work without any restrictions.
License for Published Contents
"Le Matematiche" published articlesa are distribuited with Creative Commons Attribution 4.0 International. You are free to copy, distribute and transmit the work, and to adapt the work. You must attribute the work in the manner specified by the author or licensor (but not in any way that suggests that they endorse you or your use of the work).
License for Metadata
"Le Matematiche" published articles metadata are dedicated to the public domain by waiving all publisher's rights to the work worldwide under copyright law, including all related and neighboring rights, to the extent allowed by law.
You can copy, modify, distribute and perform the work, even for commercial purposes, all without asking permission.
No Fee Charging
No fee is required to complete the submission/review/publishing process of authors paper.


